Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh

* Hướng dẫn giải

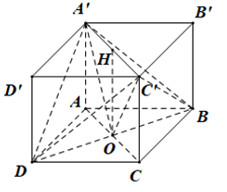
Bước 1: Xác định góc

Vì ABCD là hình vuông nên AC vuông góc BD tại O.

Suy ra \[BD \bot \left( {A'OC'} \right)\]. Góc giữa hai mặt phẳng\[\left( {A'BD} \right),\,\,\left( {C'BD} \right)\]  là\[\angle A'OC'\]

Bước 2: Sử dụng tính chất tam giác vuông cân để tính góc.

Gọi H là tâm hình vuông A′B′C′D′ thì H là trung điểm A′C′ và\[\begin{array}{*{20}{l}}{OH = A'A = a}\\{A'H = HC' = \frac{{A'C'}}{2} = \frac{{A'B'\sqrt 2 }}{2} = \frac{{a\sqrt 2 .\sqrt 2 }}{2} = a}\end{array}\]

Suy ra các tam giác\[OHA';\,\,OHC'\] vuông cân và\[\angle A'OC' = {90^ \circ }\]