Một cổng chào có dạng parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng
Câu hỏi :
Một cổng chào có dạng parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng hai sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bới parabol và mặt đất thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số \(\frac{{AB}}{{CD}}\) bằng
* Đáp án
A
* Hướng dẫn giải
Đáp án A
Chọn hệ trục tọa độ như hình vẽ
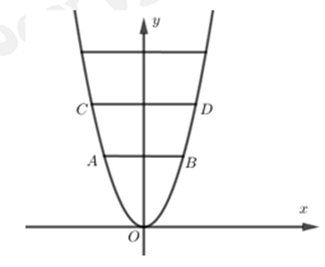
Parabol có dạng \(y = a{x^2}\), do \(\left( P \right)\) đi qua điểm \(\left( {6;18} \right) \Rightarrow a = \frac{1}{2}\).
Diện tích thiết diện của cổng trào là: \({S_0} = \int\limits_{ - 6}^6 {\left( {18 - \frac{{{x^2}}}{2}} \right)dx} = 144\)
Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là \(\frac{{{S_0}}}{3} = 48\).
Gọi \(B\left( {b;\frac{{{b^2}}}{2}} \right);{\rm{ }}D\left( {d;\frac{{{d^2}}}{2}} \right)\), khi đó \(\frac{{AB}}{{CD}} = \frac{b}{d}\)
Ta có: \(\int\limits_0^b {\left( {\frac{{{b^2}}}{2} - \frac{{{x^2}}}{2}} \right)dx} = 24 \Leftrightarrow \left. {\left( {\frac{{{b^2}x}}{2} - \frac{{{x^3}}}{6}} \right)} \right|_0^b = 24 \Rightarrow {b^3} = 72\).
Tương tự ta có \(\int\limits_0^d {\left( {\frac{{{d^2}}}{2} - \frac{{{x^2}}}{2}} \right)dx} = 48 \Rightarrow {d^3} = 144\) \( \Rightarrow \frac{{AB}}{{CD}} = \frac{1}{{\sqrt[3]{2}}}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
