Cho số phức z thỏa mãn |z-1-i|=2 . Biết rằng giá trị nhỏ nhất của

Đáp án D

Tập hợp các điểm M biểu diễn z là đường tròn \(\left( C \right)\) có tâm \(I\left( {1;1} \right)\) và bán kính \(R = 2\).

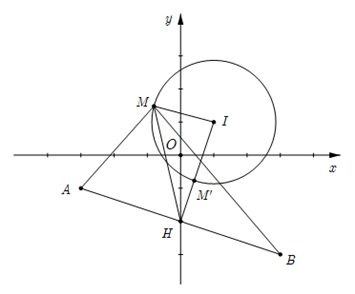
Xét \(A\left( { - 3; - 1} \right),{\rm{ }}B\left( {3; - 3} \right),{\rm{ }}H\left( {0; - 2} \right)\) là trung điểm của đoạn thẳng AB.

Ta có \(P = {\left| {z + 3 + i} \right|^2} + {\left| {z - 3 + 3i} \right|^2} = M{A^2} + M{B^2} = 2M{H^2} + \frac{{A{B^2}}}{2}\) và \(MH \ge \left| {IH - IM} \right|\).

Lại có \(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {6; - 2} \right) \Rightarrow AB = 2\sqrt {10} \\\overrightarrow {IH} = \left( { - 1; - 3} \right) \Rightarrow IH = \sqrt {10} \\IM = R = 2\end{array} \right. \Rightarrow P \ge 38 - 8\sqrt {10} \).

Dấu “=” xảy ra \( \Leftrightarrow M \equiv M' \Rightarrow a + b = 30\).