Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A,

Đáp án B

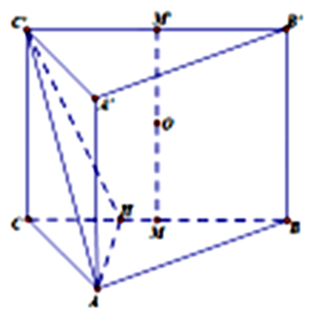
Ta có: \(AC = \sqrt {B{C^2} - A{B^2}} = a\)

Gọi \(M,M'\) lần lượt là trung điểm các cạnh \(BC,B'C'\) và O là trung điểm đoạn \(MM'\). Do M và \(M'\) là tâm đường tròn ngoại tiếp đáy hình lăng trụ \(ABC.A'B'C'\) nên O là tâm mặt cầu ngoại tiếp hình lăng trụ \(ABC.A'B'C'\).

Gọi H là hình chiếu vuông góc của A lên cạnh BC khi đó \(\widehat {\left( {AC',(BCC'B')} \right)} = \widehat {AC'H} = 30^\circ \).

Ta có: \(AH = AC'.\sin 30^\circ = \frac{1}{2}AC' \Rightarrow AC' = 2HA\) mà \(AH = \frac{{AB.AC}}{{BC}} = \frac{{a\sqrt 3 }}{2}\).

Suy ra \(AC' = a\sqrt 3 \) do \(C'{A^2} = C'{C^2} + A{C^2} \Rightarrow C'C = \sqrt {C'{A^2} - A{C^2}} = a\sqrt 2 \).

Từ đó suy ra bán kính mặt cầu ngoại tiếp cần tìm là \(R = \frac{{a\sqrt 2 }}{2}\).

Vậy diện tích cần tìm là \(S = 2\pi {a^2}\).