Tìm m để phương trình (log2(x))^2-log2(x^2)+3=m có nghiệm .

Đáp án C

Ta có \(\log _2^2x - {\log _2}{x^2} + 3 = m \Leftrightarrow \log _2^2x - 2{\log _2}x + 3 = m\). Đặt \(t = {\log _2}x\), với \(x \in \left[ {1;8} \right] \Rightarrow t \in \left[ {0;3} \right]\).

Bài toán trở thành tìm m để phương trình \({t^2} - 2t + 3 = m\) có nghiệm \(t \in \left[ {0;3} \right]\).

Xét hàm số \(f\left( t \right) = {t^2} - 2t + 3,t \in \left[ {0;3} \right]\) có đạo hàm \(f'\left( t \right) = 2t - 2 = 0 \Leftrightarrow t = 1\).

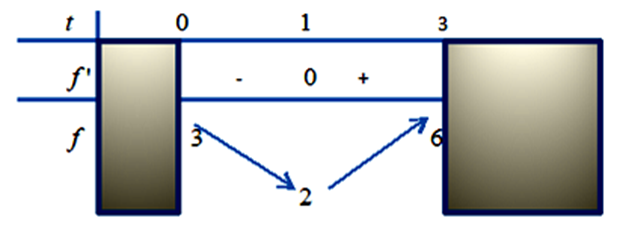
Quan sát bảng biến thiên ta có để phương trình có nghiệm \(2 \le m \le 6\).