Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, khoảng cách từ điểm A

Đáp án C

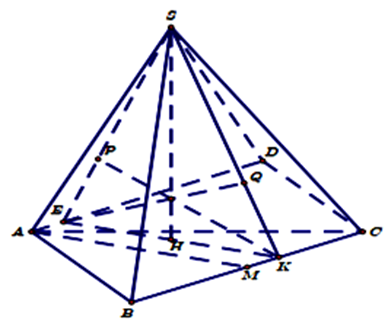
Dựng hình bình hành ABCD.

Gọi H là hình chiếu của S lên \(\left( {ABC} \right)\); E là hình chiếu của H lên AD; K là hình chiếu của H lên BC; P là hình chiếu của K lên SE; Q là hình chiếu của E lên SK.

Ta có: \(d\left( {A,(SBC)} \right) = EQ = \frac{{a\sqrt {15} }}{5}\);

\({\rm{d}}\left( {SA,BC} \right) = d\left( {BC,(SA{\rm{D}})} \right) = d\left( {K,(SA{\rm{D}})} \right) = KP = \frac{{a\sqrt {15} }}{5}\).

\( \Rightarrow KP = EQ = \frac{{a\sqrt {15} }}{5} \Rightarrow \Delta SEK\) cân tại \(S \Rightarrow H\) là trung điểm của EK.

Gọi M là trung điểm của \(BC \Rightarrow EK = AM = \frac{{a\sqrt 3 }}{2}\).

Ta có \(QK = \sqrt {E{K^2} - E{Q^2}} = \frac{{a\sqrt {15} }}{{10}}\).

\(\Delta SHK\) và \(\Delta EQK\) đồng dạng \( \Rightarrow \frac{{SH}}{{EQ}} = \frac{{HK}}{{QK}} \Rightarrow SH = \frac{{EQ.HK}}{{QK}} = \frac{{\frac{{a\sqrt {15} }}{5}.\frac{{a\sqrt 3 }}{4}}}{{\frac{{a\sqrt {15} }}{{10}}}} = \frac{{a\sqrt 3 }}{2}\).

\({V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}}}{8}\).