Cho hàm số f(x)=x^3-3x^2 . Số giá trị nguyên của m để phương trình

Đáp án D

Bảng biến thiên (I) của hàm số \(f\left( x \right) = {x^3} - 3{{\rm{x}}^2}\).

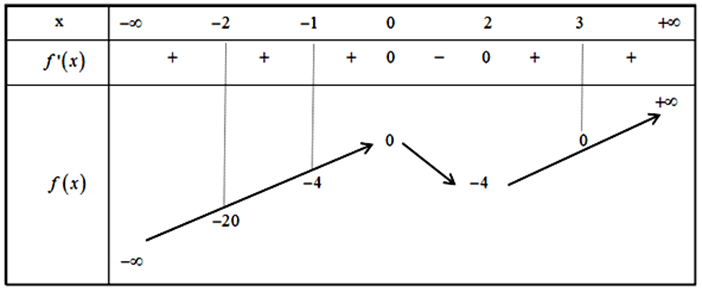
Bảng biến thiên (II) của hàm số \(g\left( x \right) = {x^4} - 4{{\rm{x}}^2} + 2\).

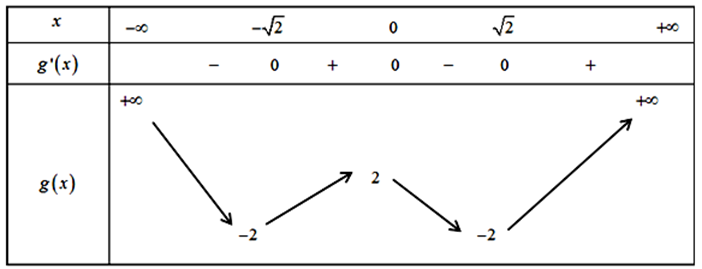
Theo BBT (1), ta xét các trường hợp:

+ Nếu \(m < - 20\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow {x^4} - 4{{\rm{x}}^2} + 2 = {k_1} < - 2\)    (2)

Theo BBT (II), phương trình (2) vô nghiệm \( \Rightarrow \) PT (1) vô nghiệm (loại).

+ Nếu \( - 20 < m < - 4\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow {x^4} - 4{{\rm{x}}^2} + 2 = {k_2} \in \left( { - 2; - 1} \right)\) (3)

Theo BBT (II), phương trình (3) có 4 nghiệm \( \Rightarrow \) PT (1) có 4 nghiệm (nhận).

+ Nếu \(m = - 4\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow \left[ \begin{array}{l}{x^4} - 4{{\rm{x}}^2} + 2 = - 1{\rm{ }}\left( 4 \right)\\{x^4} - 4{{\rm{x}}^2} + 2 = 2{\rm{ }}\left( 5 \right)\end{array} \right.\)

Theo BBT (II), PT (4) có 4 nghiệm, PT (5) có 3 nghiệm \( \Rightarrow \) PT (1) có 7 nghiệm (loại).

+ Nếu \( - 4 < m < 0\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow \left[ \begin{array}{l}{x^4} - 4{{\rm{x}}^2} + 2 = {k_3} \in \left( { - 1;0} \right){\rm{ }}\left( 6 \right)\\{x^4} - 4{{\rm{x}}^2} + 2 = {k_4} \in \left( {0;2} \right){\rm{ }}\left( 7 \right)\\{x^4} - 4{{\rm{x}}^2} + 2 = {k_5} \in \left( {2;3} \right){\rm{ }}\left( 8 \right)\end{array} \right.\)

Theo BBT (II), PT (6), (7) đều có 4 nghiệm pb, PT (8) có 2 nghiệm \( \Rightarrow \) PT (1) có 10 nghiệm (loại).

+ Nếu \(m = 0\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow \left[ \begin{array}{l}{x^4} - 4{{\rm{x}}^2} + 2 = 0{\rm{ }}\left( 9 \right)\\{x^4} - 4{{\rm{x}}^2} + 2 = 3{\rm{ }}\left( {10} \right)\end{array} \right.\)

Theo BBT (II), PT (9) có 4 nghiệm, PT (10) có 2 nghiệm \( \Rightarrow \) PT (1) có 6 nghiệm (loại).

+ Nếu \(m > 0\): \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m \Leftrightarrow {x^4} - 4{{\rm{x}}^2} + 2 = {k_6} > 3\)

Theo BBT (II), … \( \Rightarrow \) PT (1) có 2 nghiệm (loại).

Vậy PT (1) có 4 nghiệm pb khi \( - 20 < m < - 4\), mà m nguyên nên \( - 19 \le m \le - 5 \Rightarrow \) số giá trị nguyên của m là \( - 5 - \left( { - 19} \right) + 1 = 15\).