Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng

Đáp án C

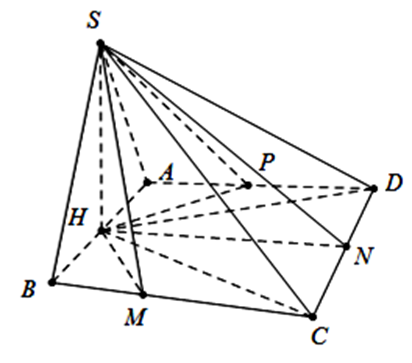
Gọi H là trung điểm của AB suy ra \(SH \bot AB\).

Do \(\left( {SAB} \right) \bot \left( {ABC{\rm{D}}} \right)\) nên \(SH \bot \left( {ABC{\rm{D}}} \right)\).

Dựng \(HM \bot BC,{\rm{ HN}} \bot {\rm{CD}},{\rm{ HP}} \bot {\rm{AD}}\).

Suy ra \(\widehat {SMH} = \widehat {SNH} = \widehat {SPH} = 60^\circ \).

Ta có: \(SH = \frac{{AB}}{2} = \frac{a}{2}\), \(HM\tan 60^\circ = HN\tan 60^\circ \)

\( = HP\tan 60^\circ = SH \Rightarrow HM = HN = HP = \frac{{a\sqrt 3 }}{6}\).

Mặt khác \({S_{ABC{\rm{D}}}} = {S_{BHC}} + {S_{CH{\rm{D}}}} + {S_{DHA}}\)

\( = \frac{1}{2}.\frac{{a\sqrt 3 }}{6}.\left( {BC + C{\rm{D}} + A{\rm{D}}} \right) = \frac{{a\sqrt 3 }}{{12}}.\left( {9{\rm{a}} - a} \right) = \frac{{2{{\rm{a}}^2}\sqrt 3 }}{3}\)

\( \Rightarrow V = \frac{1}{3}S.h = \frac{{{a^3}\sqrt 3 }}{9}\).