Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy

Đáp án B

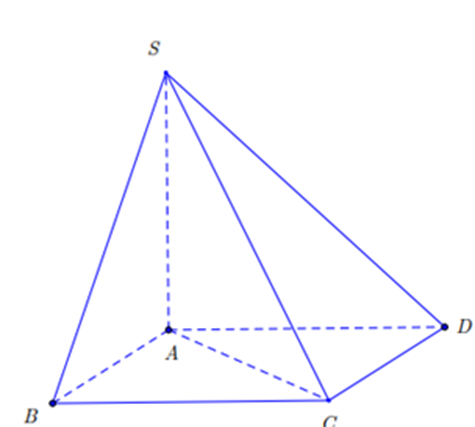
Ta có: \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = DC\\AD \subset \left( {ABCD} \right),AD \bot DC\\SD \subset \left( {SDC} \right),SD \bot DC\end{array} \right. \Rightarrow \left( {\left( {ABCD} \right),\left( {SDC} \right)} \right) = SDA = 30^\circ \)

Gọi cạnh hình vuông là x \( \Rightarrow SA = x.\tan 30^\circ = \frac{{\sqrt 3 }}{3}x\) và \(AC = \sqrt 2 a\)

Lại có \(S{C^2} = S{A^2} + A{C^2}\) hay \({\left( {a\sqrt 7 } \right)^2} = {\left( {\sqrt 2 x} \right)^2} + {\left( {\frac{{\sqrt 3 }}{3}x} \right)^2}\). Từ đó ta có \(x = \sqrt 3 a\).

Do đó \(SA = a\)

Thể tích khối chóp cần tìm là \({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.a.{\left( {\sqrt 3 a} \right)^2} = {a^3}\)