Cho hàm số f(x) có đạo hàm liên tục trên R và hàm y=f'(x)

Đáp án B

Ta có \[g'\left( x \right) = 2xf'\left( {{x^2} - 5} \right);\;g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 5} \right) = 0\end{array} \right.\].

Từ đồ thị suy ra \[\left[ \begin{array}{l}x = 0\\{x^2} - 5 = - 1\\{x^2} - 5 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 2\\x = \pm \sqrt 7 \end{array} \right.\].

Bảng biến thiên:

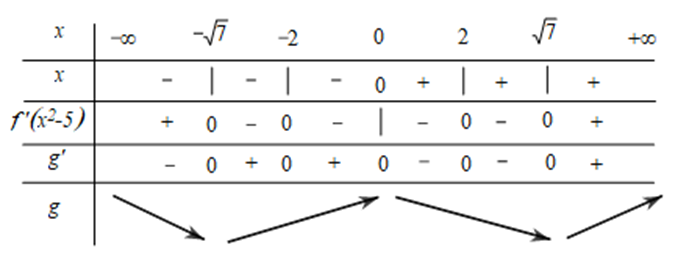
Dựa vào bảng biến thiên ta thấy hàm số \[g\left( x \right)\] đồng biến trên khoảng \[\left( { - 2;0} \right)\].