Cho hàm số y=f(x) liên tục trên R và có đạo hàm f'(x)=x^2*(x-2)*(x^2-6x+m)

Đáp án C

Phương pháp:

Hàm số nghịch biến trên \[\left( { - \infty ; - 1} \right)\] nếu \[g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\].

Cách giải:

Ta có \[\begin{array}{l}g'\left( x \right) = - f'\left( {1 - x} \right) = - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\\ = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right).\end{array}\]

Hàm số \[g\left( x \right)\] nghịch biến trên \[\left( { - \infty ; - 1} \right)\].

\[\begin{array}{l} \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\\ \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\;\left( {{\rm{do}}\;x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)} \right)\\ \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge m\;\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)\end{array}\]

Ta có: \[h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2\].

BBT

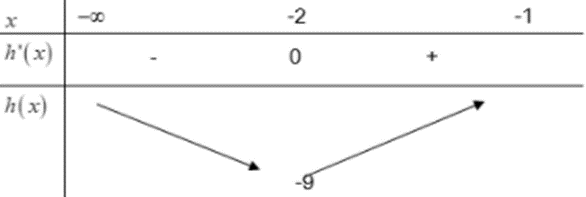
Dựa vào BBT ta có \[ - m \le - 9 \Leftrightarrow m \ge 9\].

Mà \[m \in \left[ { - 2019;2019} \right]\] và m nguyên nên \[m \in \left[ {9;10;11;...;2019} \right]\] hay có \[2019 - 9 + 1 = 2011\] giá trị của m thỏa mãn.