Cho phương trình 2^( x^3+x^2-2x+m)-2^(x^2+x)+x^3-3x+m=0

Đáp án D

\[{2^{{x^3} + {x^2} - 2x + m}} - {2^{{x^2} + x}} + {x^3} - 3x + m = 0 \Leftrightarrow {2^{{x^3} + {x^2} - 2x + m}} + \left( {{x^3} + {x^2} - 2x + m} \right) = {2^{{x^2} + x}} + \left( {{x^2} + x} \right)\;\;\;\left( 1 \right)\].

Xét hàm số \[f\left( t \right) = {2^t} + t\] với \[t \in \mathbb{R}\].

Do \[f'\left( t \right) = {2^t}.\ln 2 + 1 > 0\;\forall t \in \mathbb{R}\] nên hàm số \[f\left( t \right)\] đồng biến trên \[\mathbb{R}\].

Phương trình (1) có dạng \[f\left( {{x^3} + {x^2} - 2x + m} \right) = f\left( {{x^2} + x} \right)\].

Suy ra \[{x^3} + {x^2} - 2x + m = {x^2} + x \Leftrightarrow m = - {x^3} + 3x\;\;\;\left( 2 \right)\]

Bài toán trở thành tìm tập các giá trị m để phương trình (2) có 3 nghiệm phân biệt.

Ta có BBT của hàm số \[g\left( x \right) = - {x^3} + 3x\].

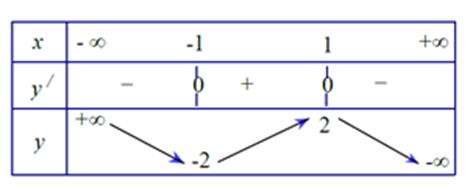
Yêu cầu bài toán \[ \Rightarrow m \in \left( { - 2;2} \right)\] hay \[a = - 2;b = 2\].

Vậy \[a + 2b = 2\].