Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ABC = 60 độ

Đáp án D

Phương pháp:

-         Gọi M là trung điểm của SD, nhận xét góc giữa SB và \[\left( {SCD} \right)\] cũng bằng góc giữa OM và \[\left( {SCD} \right)\].

-         Xác định góc \[\varphi \] và tính \[\sin \varphi \].

Cách giải:

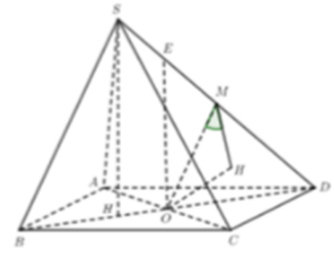
Gọi M là trung điểm của SD, nhận xét góc giữa SB và \[\left( {SCD} \right)\] cũng bằng góc giữa OM và \[\left( {SCD} \right)\] (vì \[OM//SB\]).

Gọi H là hình chiếu của O trên \[\left( {SCD} \right) \Rightarrow \left( {OM,\left( {SCD} \right)} \right) = \left( {OM,MH} \right) = OMH\].

Trong \[\left( {SBD} \right)\] kẻ \[OE//SH\], khi đó tứ diện OECD là tứ diện vuông nên \[\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{D^2}}} + \frac{1}{{O{E^2}}}\].

Ta dễ dàng tính được: \[OC = \frac{a}{2},OD = \frac{{a\sqrt 3 }}{2}\].

Lại có \[\frac{{OE}}{{SH}} = \frac{{OD}}{{HD}} = \frac{3}{4} \Rightarrow OE = \frac{3}{4}SH\], mà \[SH = \sqrt {S{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\].

Do đó \[OE = \frac{3}{4}SH = \frac{3}{4}.\frac{{a\sqrt 6 }}{3} = \frac{{a\sqrt 6 }}{4}\].

Suy ra \[\frac{1}{{O{H^2}}} = \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{4}} \right)}^2}}} = \frac{8}{{{a^2}}} \Rightarrow OH = \frac{{a\sqrt 2 }}{4}\].

Tam giác OMH vuông tại H có \[OM = \frac{1}{2}SB = \frac{a}{2};OH = \frac{{a\sqrt 2 }}{4} \Rightarrow \sin OMH = \frac{{OH}}{{OM}} = \frac{{\sqrt 2 }}{2}\].

Vậy \[\sin \varphi = \frac{{\sqrt 2 }}{2}\]