Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E, F lần lượt là trung điểm

* Hướng dẫn giải

Đáp án A

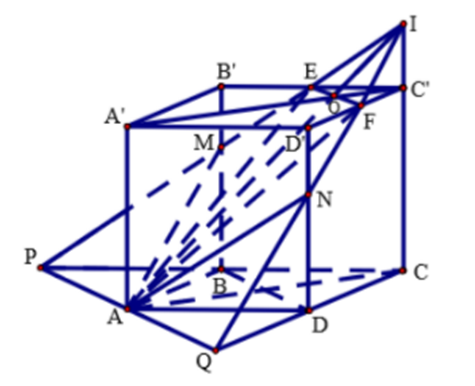
Dựng thiết diện: PQ qua A và song song với BD (vì \[EF//B'D'//BD\]).

PE cắt các cạnh BB’, CC’ tại M và I. Tương tự ta tìm được giao điểm N. Thiết diện là AMEFN.

Dựa vào đường trung bình BD và định lí Ta-lét cho các tam giác IAC, DNQ, D’NF ta tính được: \[IC' = \frac{a}{3},ND = \frac{{2a}}{3}\]. Tương tự ta tính được: \[MB = \frac{{2a}}{3}\]. Và ta có: \[QD = PB = a\].

Ta có \[{V_{IEFC'}} = \frac{1}{3}.\frac{a}{3}.\frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^3}}}{{72}}\]. Dùng tỉ lệ thể tích ta có: \[{V_{IPQC}} = {4^3}.{V_{IEFC'}} = 64.\frac{{{a^3}}}{{72}} = \frac{{8{a^3}}}{9}\]

\[{V_{NADQ}} = \frac{1}{3}.\frac{{2a}}{3}.\frac{1}{2}.a.a = \frac{{{a^3}}}{9} = {V_{MPAB}} \Rightarrow {V_2} = \frac{{8{a^3}}}{9} - \frac{{{a^3}}}{{72}} - 2.\frac{{{a^3}}}{9} = \frac{{47{a^3}}}{{72}}\].

Thể tích khối lập phương ABCD.A’B’C’D’ là \[{a^3}\] nên \[{V_1} = {a^3} - \frac{{47{a^3}}}{{72}} = \frac{{25{a^3}}}{{72}}\].

\[ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{25}}{{47}}\].