Cho hình chóp đều S.ABCD có cạnh AB=a , góc giữa đường thẳng SA

Đáp án B

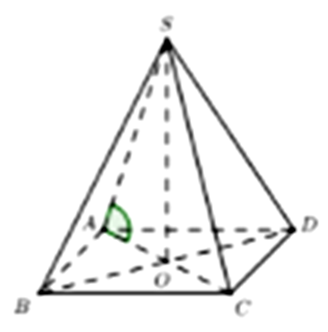
+ Gọi \(O = AC \cap B{\rm{D}}\) ta có \[{\rm{S}}O \bot \left( {ABC{\rm{D}}} \right)\].

+ Xác định góc giữa SA và mặt phẳng \(\left( {ABC} \right)\), từ đó tính SO.

+ Sử dụng công thức tính thể tích \(V = \frac{1}{3}AO.{S_{ABC{\rm{D}}}}\).

Gọi \(O = AC \cap B{\rm{D}}\) ta có \(SO \bot \left( {ABC{\rm{D}}} \right)\).

\( \Rightarrow \angle \left( {SA;(ABC)} \right) = \angle \left( {SA;(ABC{\rm{D}})} \right) = \angle SAO = 45^\circ \Rightarrow SO = OA = \frac{{a\sqrt 2 }}{2}\).

\( \Rightarrow {V_{S.ABC{\rm{D}}}} = \frac{1}{3}SO.{S_{ABC{\rm{D}}}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\).