Cho đồ thị hàm số y=x^3-6x^2+9x-2 như hình vẽ

Đáp án B

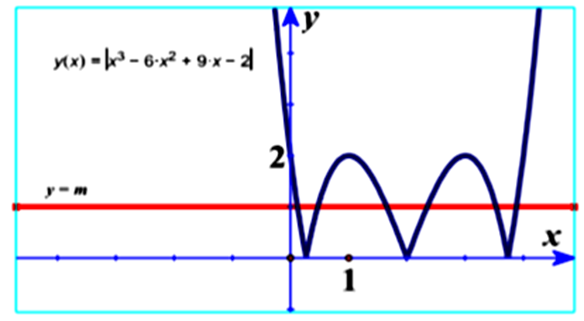
Đồ thị hàm số \(y = \left| {{x^3} - 6{{\rm{x}}^2} + 9{\rm{x}} - 2} \right|\) có được bằng cách biến đổi đồ thị \(\left( C \right)\) hàm số \(y = {x^3} - 6{{\rm{x}}^2} + 9{\rm{x}} - 2\).

Giữ nguyên phần đồ thị \(\left( C \right)\) nằm trên trục hoành.

Lấy đối xứng phần đồ thị của \(\left( C \right)\) phần dưới trục hoành qua trục hoành.

Xóa phần đồ thị còn lại \(\left( C \right)\) phía dưới trục hoành.

Số nghiệm của phương trình \(\left| {{x^3} - 6{{\rm{x}}^2} - 9{\rm{x}} - 2} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^3} - 6{{\rm{x}}^2} + 9{\rm{x}} - 2} \right|\) và đồ thị hàm số \(y = m\). Để phương trình có 6 nghiệm phân biệt thì điều kiện cần và đủ là \(0 < m < 2\).