Có bao nhiêu số nguyên a thuộc (-2019, 2019) để phương trình

Đáp án D

Phương trình \(\frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} = x + a \Leftrightarrow \frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} - x = a\)

Đặt hàm số \(f\left( x \right) = \frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} - x\) có tập xác định \(D = \left( { - 5; - 4} \right) \cup \left( { - 4;0} \right) \cup \left( {0;\infty } \right)\)

Ta có: \(f'\left( x \right) = \frac{{ - 1}}{{\left( {x + 5} \right){{\ln }^2}\left( {x + 5} \right)}} - \frac{{{3^x}\ln 3}}{{{{\left( {{3^x} - 1} \right)}^2}}} - 1 < 0\)

\( \Rightarrow f\left( x \right)\) nghịch biến trên các khoảng của tập xác định.

Các giới hạn: \(\mathop {\lim }\limits_{x \to - {5^ + }} f\left( x \right) = \frac{1}{{{3^{ - 5}} - 1}} + 5 = \frac{{967}}{{242}},{\rm{ }}\mathop {\lim }\limits_{x \to - {4^ - }} f\left( x \right) = - \infty ,{\rm{ }}\mathop {\lim }\limits_{x \to - {4^ + }} f\left( x \right) = + \infty \)

\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - \infty ,{\rm{ }}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty ,{\rm{ }}\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \).

Bảng biến thiên

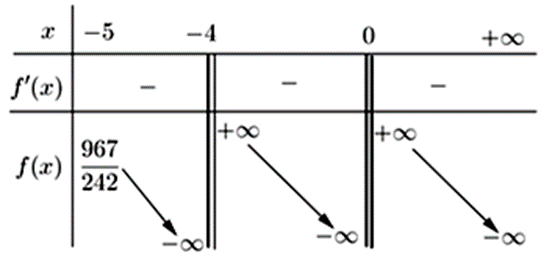
Phương trình \(f\left( x \right) = a\) có hai nghiệm phân biệt khi và chỉ khi \(a \ge \frac{{967}}{{242}}\).

Do \(\left\{ \begin{array}{l}a \in \mathbb{Z}\\a \in \left( { - 2019;2019} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a \in \mathbb{Z}\\a \in \left[ {4;2018} \right]\end{array} \right.\). Vậy có \(2018 - 4 + 1 = 2015\) giá trị của a.