Cho hình thang vuông ABCD (vuông tại A và D) có độ dài các cạnh là

Đáp án C

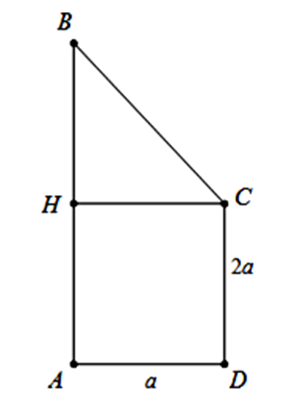
Gọi H là hình chiếu của C trên AB.

\( \Rightarrow A{\rm{D}}CH\) là hình chữ nhật \( \Rightarrow AH = 2{\rm{a}},BH = 2{\rm{a}}\).

Khi quay hình thang ABCD quanh trục AB, ta được:

Khối trụ thể tích \({V_1}\), có chiều cao \({h_1} = AH = 2{\rm{a}}\), bán kính đường tròn đáy \(r = A{\rm{D}} = a \Rightarrow {V_1} = 2\pi {a^3}\).

Khối nón thể tích \({V_2}\), có chiều cao \({h_2} = BH = 3{\rm{a}}\), bán kính đường tròn đáy \(r = CH = a \Rightarrow {V_2} = \pi {a^3}\).

Vậy thể tích khối tròn xoay cần tìm là \(V = {V_1} + {V_2} = 3\pi {a^3}\).