Cho hình chóp S.ABCD có SA vuông góc với đáy, SA=a căn 6 Đáy ABCD là hình thang
Câu hỏi :
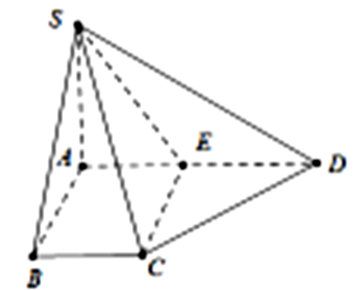
Cho hình chóp S.ABCD có SA vuông góc với đáy, \[SA = a\sqrt 6 .\] Đáy ABCD là hình thang vuông tại A và \[B,{\mkern 1mu} {\mkern 1mu} AB = BC = \frac{1}{2}AD = a.\] Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp \[S.ECD\].
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Ta có: \({\rm{CE // AB}} \Rightarrow {\rm{CE}} \bot A{\rm{D}}\)
Mặt khác \(CE \bot {\rm{S}}A \Rightarrow CE \bot \left( {SE{\rm{D}}} \right)\)
\( \Rightarrow {R_{C.SE{\rm{D}}}} = \sqrt {\frac{{C{E^2}}}{4} + {{\left( {{R_{S{\rm{D}}E}}} \right)}^2}} \)
Lại có \(CE = AB = a,{\rm{ }}\sin \widehat {SE{\rm{A}}} = \sin \widehat {SE{\rm{D}}}\)
\[ = \frac{{SA}}{{SE}} = \frac{{a\sqrt 6 }}{{\sqrt {{a^2} + 6{{\rm{a}}^2}} }} = \frac{{a\sqrt 6 }}{{\sqrt 7 }}\]
\( \Rightarrow {R_{SE{\rm{D}}}} = \frac{{S{\rm{D}}}}{{2\sin \widehat {SE{\rm{D}}}}} = \frac{{a\sqrt {10} }}{{2.\frac{{a\sqrt 6 }}{{\sqrt 7 }}}} = \frac{{a\sqrt {105} }}{6}\)
Vậy \({R_{S.C{\rm{D}}E}} = a\sqrt {\frac{{19}}{6}} \).
Cách 2: Do \(\left( {SE{\rm{D}}} \right) \bot \left( {CE{\rm{D}}} \right) \Rightarrow R = \sqrt {R_1^2 + R_2^2 - \frac{{G{T^2}}}{4}} \) trong đó \({R_1} = {R_{SE{\rm{D}}}} = \frac{{a\sqrt {105} }}{6}\),
\({R_2} = {R_{CE{\rm{D}}}} = \frac{{C{\rm{D}}}}{2} = \frac{{a\sqrt 2 }}{2}\) và \(GT = E{\rm{D}} = a \Rightarrow R = a\sqrt {\frac{{19}}{6}} \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
