Trong khôn gian tọa độ Oxyz, cho mặt cầu (S): (x-1)^2+(y-2)^2+(z-3)^2=14/3

Đáp án A

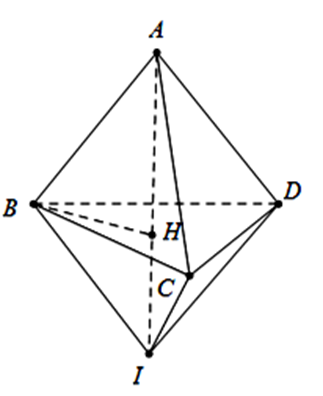
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {\frac{{14}}{3}} \)

Vì AB là tiếp tuyến nên \(AB \bot BI\), lại có \(IB = IC = I{\rm{D}} = R\) nên AI là trục đường tròn ngoại tiếp tam giác BCD

Gọi \(H = AI \cap \left( {BC{\rm{D}}} \right)\), đặt \(AB = a = C{\rm{D}} \Rightarrow HB = \frac{{a\sqrt 3 }}{3}\)

\(\sin \widehat {HAB} = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}\) mà \(\Delta ABI\) vuông tại B nên

\(AI.\sin \widehat {HBA} = BI = \sqrt {\frac{{14}}{3}} \Rightarrow AI = \sqrt {14} \)

Gọi \(A\left( {1 + 3t;2 + 2t;3 + t} \right)\) ta có \(A{I^2} = 14{t^2} = 14\)

\( \Rightarrow \left[ \begin{array}{l}t =  - 1\\t = 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}A\left( { - 2;0;2} \right){\rm{ }}\left( {loai} \right)\\A\left( {4;4;4} \right)\end{array} \right. \Rightarrow OA = 4\sqrt 3 \).