Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;2; - 3),B( - 2; - 2;1) và mặt phẳng

Đáp án C

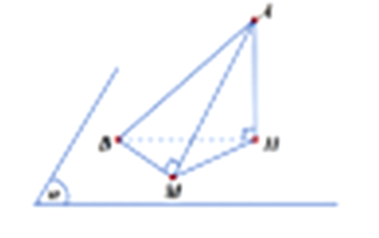
Dễ thấy \(B \in \left( \alpha \right)\), gọi H là hình chiếu của A lên \(\left( \alpha \right) \Rightarrow H\left( { - 3; - 2; - 1} \right)\).

Ta có \(AH \bot \left( \alpha \right) \Rightarrow AH \bot MB\) và \(AM \bot MB\) (do \(\widehat {AMB} = 90^\circ \)) \( \Rightarrow MB \bot MH \Rightarrow MB \le BH\).

Dấu “=” xảy ra khi \(M \equiv H \Leftrightarrow \) đường thẳng MB đi qua \(B\left( { - 2; - 2;1} \right)\) và \(H\left( { - 3; - 2; - 1} \right)\).

Suy ra \(MB:\left\{ \begin{array}{l}x = - 2 + t\\y = - 2\\z = 1 + 2t\end{array} \right.\).