Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:x-2/-1=y-1/3=z-1/2

Đáp án C

Gọi A là giao điểm của \({d_1}\) và \(\left( P \right),B\) là giao điểm của \({d_2}\) và \(\left( P \right).\)

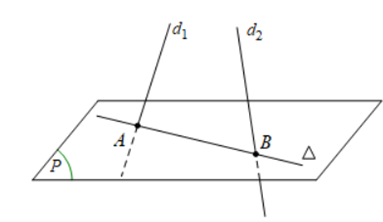
Ta có: \(A\left( {2 - a;1 + 3a;1 + 2a} \right) \in {d_1},\) cho điểm A thuộc \(\left( P \right)\) thì

\(2 - a + 2\left( {1 + 3a} \right) - 3\left( {1 + 2a} \right) - 2 = 0\)

\( \Leftrightarrow - 1 - a = 0 \Leftrightarrow a = - 1 \Rightarrow A\left( {3; - 2; - 1} \right)\)

Điểm \(B\left( {1 - 3b; - 2 + b; - 1 - b} \right) \in {d_2}\), cho B thuộc \(\left( P \right)\) thì \(1 - 3b + 2\left( { - 2 + b} \right) + 3 + 3b - 2 = 0\)

\( \Leftrightarrow 2b - 2 = 0 \Leftrightarrow b = 1 \Rightarrow B\left( { - 2; - 1; - 2} \right)\)

Đường thẳng cần tìm là AB, vectơ chỉ phương của \(AB\) là \(\overrightarrow u = \overrightarrow {AB} \left( { - 5;1; - 1} \right).\)

Vậy \(\Delta :\frac{{x - 3}}{{ - 5}} = \frac{{y + 2}}{1} = \frac{{z + 1}}{{ - 1}}.\)