Trong không gian Oxyz, cho hai điểm A(2;-2;4), B(-3;3;-1) và mặt cầu
Câu hỏi :
Trong không gian Oxyz, cho hai điểm \[A\left( {2; - 2;4} \right),B\left( { - 3;3; - 1} \right)\] và mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 3\]. Xét điểm M thay đổi thuộc mặt cầu (S), giá trị nhỏ nhất của \[2M{A^2} + 3M{B^2}\] bằng
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Mặt cầu \(\left( S \right)\) có tâm \(J\left( {1;3;3} \right),R = \sqrt 3 .\)
Gọi I là điểm thỏa mãn \(2\overrightarrow {IA} + 3\overrightarrow {IB} = \overrightarrow 0 \Rightarrow I\left( { - 1;1;1} \right)\) và \(\overrightarrow {IJ} = \left( {2;2;2} \right) \Rightarrow IJ = 2\sqrt 3 .\)
Khi đó \(P = 2M{A^2} + 3M{B^2} = 2{\left( {\overrightarrow {MA} } \right)^2} + 3{\left( {\overrightarrow {MB} } \right)^2} = 2{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 3{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2}\)
Suy ra \(P = 5M{I^2} + 2I{A^2} + 3I{B^2} + 2\overrightarrow {MI} \left( {\underbrace {2\overrightarrow {IA} + 3\overrightarrow {IB} }_{\overrightarrow 0 }} \right)\)
Do đó \({P_{\min }} \Leftrightarrow M{I_{\min }}.\) Ta có hình minh họa sau:
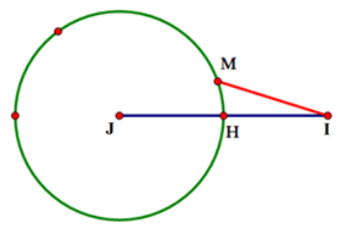
Khi đó \(M{I_{\min }} \Leftrightarrow MI = IH \Rightarrow I \equiv H\) với H là trung điểm IJ.
Khi đó ta có \(IM = \frac{{IJ}}{2} = \frac{{2\sqrt 3 }}{2} = \sqrt 3 .\) Đồng thời \(\left\{ \begin{array}{l}IA = 3\sqrt 3 \\IB = 2\sqrt 3 \end{array} \right.\)
Do đó \({P_{\min }} = 5M{I^2} + 2I{A^2} + 3I{B^2} = 5.3 + 2.27 + 3.12 = 105\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
