Cho hình chóp S.ABCD có chiều cao bằng 9 và đáy là hình bình hành
Câu hỏi :
Cho hình chóp S.ABCD có chiều cao bằng 9 và đáy là hình bình hành có diện tích bằng 27. Gọi \[M,N,P,Q\] lần lượt là các trọng tâm của các mặt bên SAB, SBC, SCD, SDA. Tính thể tích khối đa diện lồi có các đỉnh \[A,B,C,D,M,N,P,Q\].
* Đáp án
B
* Hướng dẫn giải
Đáp án B
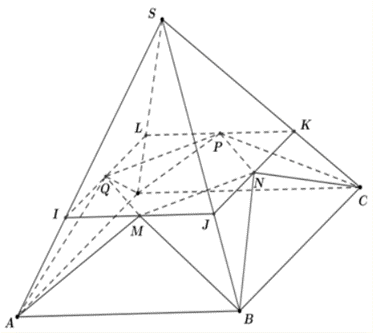
Thể tích khối chóp \({V_{S.ABCD}} = \frac{1}{3}.9.27 = 81.\)
Gọi I, J, K, L lần lượt là giao điểm của mặt phẳng \(\left( {MNPQ} \right)\) và SA, SB, SC, SD.
Vì \(IJKL\) đồng dạng với ABCD theo tỉ số \(\frac{2}{3}\) nên \({S_{IJKL}} = \frac{4}{9}{S_{ABCD}}.\)
Thể tích các khối chóp AIMQ, BJMN, CKNP, DLPQ bằng nhau và bằng
\({V_2} = \frac{1}{3}.{S_{IMQ}}.d\left( {A,\left( {IMQ} \right)} \right) = \frac{1}{3}.\frac{1}{8}.{S_{MBPQ}}.\frac{1}{3}.d\left( {S,\left( {ABCD} \right)} \right)\)
\( = \frac{1}{3}.\frac{1}{8}.\frac{4}{9}.{S_{ABCD}}.\frac{1}{3}.d\left( {S,\left( {ABCD} \right)} \right) = \frac{1}{{54}}.81 = \frac{3}{2}.\)
Thể tích \({V_1} = {V_{IJKL.ABCD}} = {V_{S.ABCD}} - {V_{S.IJKL}} = {V_{S.ABCD}} - \frac{1}{3}.{S_{IJKL}}.d\left( {S,\left( {IJKL} \right)} \right)\)
\( = {V_{S.ABCD}} - \frac{1}{3}.\frac{4}{9}.{S_{ABCD}}.\frac{2}{3}.d\left( {S,\left( {ABCD} \right)} \right) = \frac{{19}}{{27}}{V_{S.ABCD}} = 57.\)
Vậy thể tích cần tính bằng \(V = {V_1} - 4{V_2} = 57 - 4.\frac{3}{2} = 51.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
