Trong không gian Oxyz, cho mặt phẳng (P): 2x+2y-z+9=0

Đáp án D

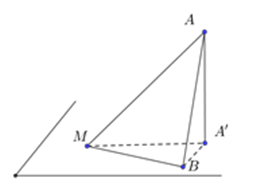
Ta có đường thẳng \[d:x = 1 + 3t;{\rm{ }}y = 2 + 4t;{\rm{ }}z = - 3 - 4t\]. Đường thẳng \[d\] cắt \[\left( P \right)\] tại \[B\left( { - 2; - 2;1} \right)\].

Gọi \[A'\] là hình chiếu của \[\left( A \right)\] lên \[\left( P \right)\] thì \[AA':y = 1 + 2t;{\rm{ }}y = 2 + 2t;{\rm{ }}z = - 3 - t\].

Suy ra \[A'\left( { - 3; - 2; - 1} \right)\]. Theo định lí Pitago kết hợp \[AM \ge AA'\] ta có

\[M{A^2} + M{B^2} = A{B^2} \Rightarrow M{B^2} = A{B^2} - M{A^2} \le A{B^2} - A'{A^2} = A'{B^2}\]

Dấu đẳng thức xảy ra khi \[M \equiv A' \Rightarrow MB = A'B = \sqrt 5 \].