Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, AB = AC = a, AA’ =

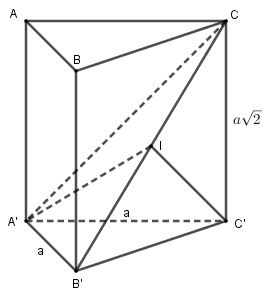
Ta có:

\[\begin{array}{*{20}{l}}{A'B' = AB = a}\\{B'C' = \sqrt {A'{B^{\prime 2}} + A'{C^{\prime 2}}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 }\\{B'C = \sqrt {B'{C^{\prime 2}} + C'{C^2}} = \sqrt {2{a^2} + 2{a^2}} = 2a}\\{A'C = \sqrt {A'{C^{\prime 2}} + C'{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 }\\{ \Rightarrow A'{B^{\prime 2}} + A'{C^2} = {a^2} + 3{a^2} = 4{a^2} = B'{C^2}}\end{array}\]

\[ \Rightarrow \Delta A\prime B\prime C\] vuông tại AA′.

Gọi I là trung điểm của B′C thì IB′ = IC = IA′

Mà \[\Delta CC\prime B\prime \;\] vuông tại C′ nên  IB′ = IC = IC′

Vậy I là tâm mặt cầu ngoại tiếp tứ diện CA′B′C′ và bán kính \[R = \frac{1}{2}B'C = a\]

\[ \Rightarrow S = 4\pi {R^2} = 4\pi {a^2}\]