Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại BB có cạnh AB=3, BC=4và góc giữa DC và mặt phẳng (ABC) bằng 450. Tính thể tích mặt cầu ngoại tiếp...

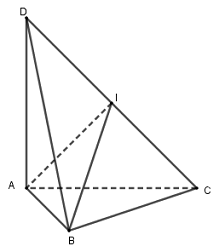
Ta có : \(\left\{ {\begin{array}{*{20}{c}}{BC \bot BA}\\{BC \bot DA}\end{array}} \right. \Rightarrow BC \bot (ABD) \Rightarrow BC \bot BD \Rightarrow \Delta BCD\) vuông tại B.

Gọi I là trung điểm của CD thì \[IB = IC = ID = \frac{1}{2}CD\]

Tam giác ACD vuông tại A nên \[IA = IC = ID = \frac{1}{2}CD\]

Do đó \[IA = IB = IC = ID \Rightarrow I\]  là tâm mặt cầu ngoại tiếp tứ diện ABCDABCD.

Tam giác ABC vuông tại B nên \[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {4^2}} = 5\] (Định lí Pytago).

Vì\[DA \bot \left( {ABC} \right)\] nên ACAC là hình chiếu của DCDC lên (ABC).\[ \Rightarrow \angle \left( {DC;\left( {ABC} \right)} \right) = \angle \left( {DC;AC} \right) = \angle DCA = {45^0}\]

Tam giác DAC vuông tại A có \[\widehat {DCA} = {45^0}\] nên là tam giác vuông cân

\[ \Rightarrow DC = AC\sqrt 2 = 5\sqrt 2 \]

\[ \Rightarrow R = IA = \frac{1}{2}DC = \frac{{5\sqrt 2 }}{2}\]

Vậy thể tích khối cầu ngoại tiếp tứ diện ABCD là :\[V = \frac{4}{3}\pi I{A^3} = \frac{4}{3}\pi .{\left( {\frac{{5\sqrt 2 }}{2}} \right)^3} = \frac{{125\sqrt 2 }}{3}\pi \]