Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:

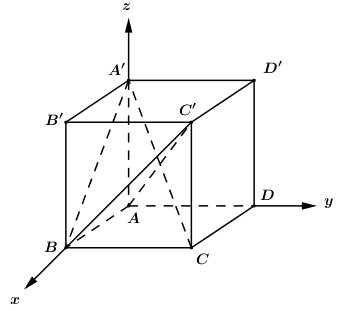
Gắn hệ trục tọa độ như hình vẽ, coi hình lập phương có cạnh bằng 1 ta có:

\[A\left( {0;0;0} \right),B\left( {1;0;0} \right),C\left( {1;1;0} \right),A'\left( {0;0;1} \right),C'\left( {1;1;1} \right)\]

Ta có:\[\overrightarrow {A'B} = \left( {1;0; - 1} \right),\,\,\overrightarrow {BC} = \left( {0;1;0} \right) \Rightarrow \left[ {\overrightarrow {A'B} ;\overrightarrow {BC} } \right] = \left( {1;0;1} \right) \Rightarrow \left( {A'BC} \right)\] có 1 VTPT là\[\overrightarrow {{n_1}} = \left( {1;0;1} \right)\]

\[\overrightarrow {AB} = \left( {1;0;0} \right),\,\,\overrightarrow {AC'} = \left( {1;1;1} \right) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC'} } \right] = \left( {0; - 1;1} \right) \Rightarrow \left( {ABC'} \right)\]có 1 VTPT là\[\overrightarrow {{n_2}} = \left( {0; - 1;1} \right)\]

Gọi αα là góc giữa hai mặt phẳng (A′BC) và (ABC′) ta có:

\[\cos \alpha = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {1.0 + 0.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{1}{2}\]