Cho hàm số f(x)=ax^3+bx^2+cx+d (a,b,c,d thuộc R) có đồ thị như hình vẽ bên

Câu hỏi :

Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\left( {a,b,c,d \in \mathbb{R}} \right)\] có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình \[2f\left( {\left| x \right|} \right) - m = 0\] có đúng bốn nghiệm thực phân biệt.

* Đáp án

C

* Hướng dẫn giải

Đáp án C

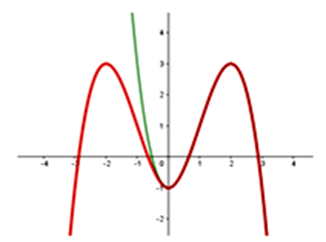
Lấy đối xứng đồ thị \(f\left( x \right)\) qua trục tung, bỏ đi phần \(x > 0\).

Phương trình tương đương \(f\left( {\left| x \right|} \right) = 0,5m\). Để có 4 nghiệm phân biệt thì \( - 1 < 0,5m < 3 \Rightarrow - 2 < m < 6\).