Trong không gian tọa độ Oxyz, cho mặt cầu (S1) có tâm I1(1;0;1)
Câu hỏi :
Trong không gian tọa độ Oxyz, cho mặt cầu \[\left( {{S_1}} \right)\] có tâm \[{I_1}\left( {1;0;1} \right),\;\] bán kính \[{R_1} = 2\] và mặt cầu \[\left( {{S_2}} \right)\] có tâm \[{I_2}\left( {1;3;5} \right),\] bán kính \[{R_2} = 1.\] Đường thẳng d thay đổi nhưng luôn tiếp xúc với \[\left( {{S_1}} \right),\;\left( {{S_2}} \right)\] lần lượt tại A và B. Gọi \[M,\;m\] lần lượt là giá trị lớn nhất và nhỏ nhất của đoạn AB. Tính giá trị của \[P = M.m\]
* Đáp án
D
* Hướng dẫn giải
Đáp án D
Ta có \({I_1}{I_2} = 5 > {R_1} + {R_2} = 3,{\rm{ }}{{\rm{I}}_1}A{\rm{ // }}{{\rm{I}}_2}B\).
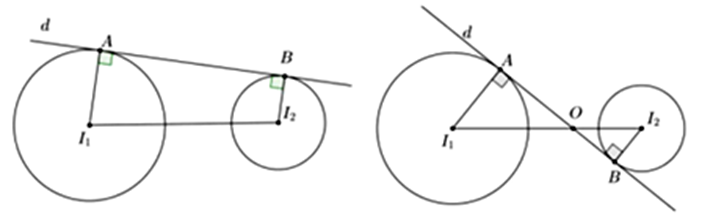
Ta có \({I_1}I_2^2 = {\left( {\overrightarrow {{I_1}A} + \overrightarrow {AB} + \overrightarrow {B{I_2}} } \right)^2} = R_1^2 + A{B^2} + R_2^2 + 2\overrightarrow {{I_1}A} .\overrightarrow {B{I_2}} \)
\( \Rightarrow A{B^2} = 20 + 2\overrightarrow {{I_1}A} .\overrightarrow {{I_2}B} = 20 + 2.2.1.\cos \left( {\overrightarrow {{I_1}A} ,\overrightarrow {{I_2}B} } \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}\max AB = 2\sqrt 6 \Leftrightarrow \overrightarrow {{I_1}A} {\rm{ }} \nearrow \nearrow {\rm{ }}\overrightarrow {{I_2}B} \\\min AB = 4 \Leftrightarrow \overrightarrow {{I_1}A} {\rm{ }} \nearrow \swarrow {\rm{ }}\overrightarrow {{I_2}B} \end{array} \right.\).
Vậy \(P = 2\sqrt 6 .4 = 8\sqrt 6 \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
