Cho hình chóp đều SBAC có AB=2a , khoảng cách từ A đến

Đáp án D

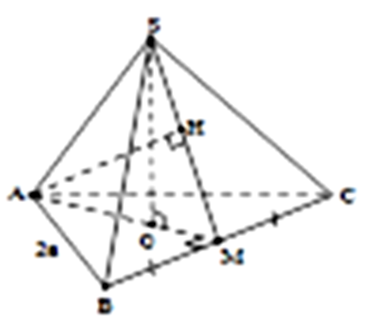
Gọi M là trung điểm của BC và G là tâm đường tròn ngoại tiếp \(\Delta ABC\).

Do S.ABC là hình chóp đều nên \(SG \bot \left( {ABC} \right)\) và G là trọng tâm \(\Delta ABC\).

Ta có: \(\left\{ \begin{array}{l}AM \bot BC\\SG \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right)\) hay \(\left( {SBC} \right) \bot \left( {SAM} \right)\) theo giao tuyến SM.

Trong \(\left( {SAM} \right)\), kẻ \(AH \bot {\rm{S}}M,H \in SM \Rightarrow AH \bot \left( {SBC} \right)\).

Vậy \(d\left( {A,(SBC)} \right) = AH = \frac{{3{\rm{a}}}}{2}\).

Vì \(\Delta ABC\) là tam giác đều cạnh 2a nên \(AM = \frac{{2{\rm{a}}\sqrt 3 }}{2} = a\sqrt 3 \) và \({S_{\Delta ABC}} = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \).

Đặt \(SG = x\). Ta có: \(GM = \frac{1}{3}AM = \frac{1}{3}.a\sqrt 3 = \frac{{a\sqrt 3 }}{3}\).

Xét \(\Delta SGM\) vuông tại G ta có: \(SM = \sqrt {S{G^2} + G{M^2}} = \sqrt {{x^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} \)

Xét \(\Delta SAM\) ta có: \({S_{\Delta SAM}} = \frac{1}{2}SG.AM = \frac{1}{2}AH.SM \Rightarrow x.a\sqrt 3 = \frac{{3{\rm{a}}}}{2}\sqrt {{x^2} + \frac{{{a^2}}}{3}} \)

\( \Leftrightarrow 4{{\rm{x}}^2} = 3\left( {{x^2} + \frac{{{a^2}}}{3}} \right) \Leftrightarrow x = a\). Do đó: \(SG = a\).

Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}SG.{S_{\Delta ABC}} = \frac{1}{3}.a.{a^2}\sqrt 3 = \frac{{{a^3}\sqrt 3 }}{3}\).