Cho z1,z2 là hai trong các số phức thỏa mãn |z-3+căn 3*i| =2

Đáp án A

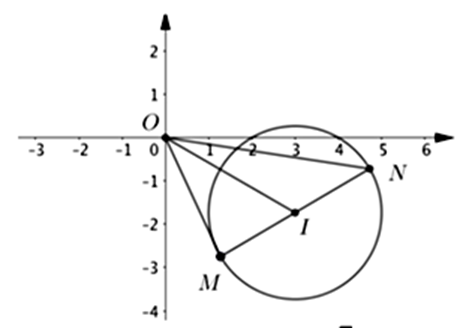
Tập hợp điểm biểu diễn số phức z là đường tròn \(\left( C \right)\) tâm \(I\left( {3; - \sqrt 3 } \right),R = 2\). Gọi M, N lần lượt biểu diễn hai số phức \({z_1},{z_2}\) thì \(MN = \left| {{z_1} - {z_2}} \right| = 4 = 2{\rm{R}}\), suy ra MN là đường kính của \(\left( C \right)\).

Chú ý môđun mỗi số phức chính là các khoảng cách OM, ON.

Áp dụng bất đẳng thức Bunyakovsky kết hợp công thức trung tuyến tam giác OMA ta có:

\(\left| {{z_1}} \right| + \left| {{z_2}} \right| = OM + ON \le \sqrt {2\left( {O{M^2} + O{N^2}} \right)} = \sqrt {4{\rm{O}}{I^2} + M{N^2}} = 8\).