Cho hàm số y=f(x) xác định trên R có f(-3)>8

Đáp án C

Xét hàm số \(g\left( x \right) = 2f\left( x \right) - {\left( {x - 1} \right)^2}\) ta có \(g'\left( x \right) = 2f'\left( x \right) - 2\left( {x - 1} \right) = 0 \Leftrightarrow f'\left( x \right) = x - 1\)

Vẽ đồ thị hàm số \(y = f'\left( x \right)\) và \(y = x - 1\) trên cùng một hệ trục tọa độ ta thấy \(f'\left( x \right) = x - 1 \Leftrightarrow x = - 1\), \(x = 1,{\rm{ }}x = 2,{\rm{ }}x = 3\) (trong đó \(x = 1\) là nghiệm kép) ta có BBT sau:

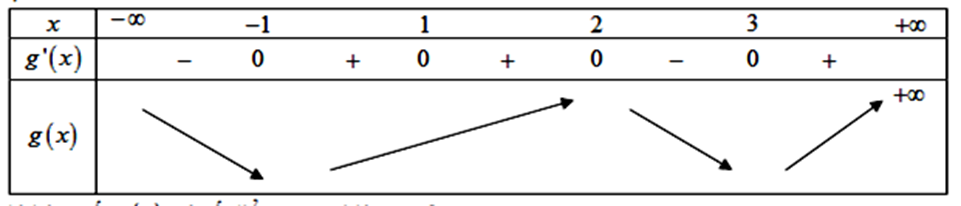
Khi đó hàm số \(g\left( x \right)\) có số điểm cực trị là \(m = 3\).

Lại có \(g\left( { - 3} \right) = 2f\left( { - 3} \right) - 16 = 2\left[ {f\left( { - 3} \right) - 8} \right] > 0,{\rm{ g}}\left( 4 \right) = 2f\left( 4 \right) - 9 > 0\) và \(g\left( 2 \right) = 2f\left( 2 \right) - 1 < 0\).

Do đó phương trình \(g\left( x \right) = 0\) có 2 nghiệm phân biệt nên \(n = 2\).

Số điểm cực trị của hàm số \(y = \left| {g\left( x \right)} \right| = \left| {2f\left( x \right) - {{\left( {x - 1} \right)}^2}} \right|\) bằng \(m + n = 5\).