Trong không gian Oxyz, cho đường thẳng d: x-1/2=y/1=z-1/1
Câu hỏi :
Trong không gian Oxyz, cho đường thẳng \[d:\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z - 1}}{1}\] và mặt cầu \[(S):{\left( {x - 4} \right)^2} + {\left( {y - 5} \right)^2} + {\left( {z - 7} \right)^2} = 2.\] Hai điểm \[A,B\] thay đổi trên (S) sao cho tiếp diện của (S) tại A và B vuông góc với nhau. Đường thẳng qua A song song với d cắt mặt phẳng \[(Oxy)\] tại M, đường thẳng qua B song song với d cắt mặt phẳng \[(Oxy)\] tại N. Tìm giá trị lớn nhất của tổng \[AM + BN.\]
* Đáp án
A
* Hướng dẫn giải
Đáp án A
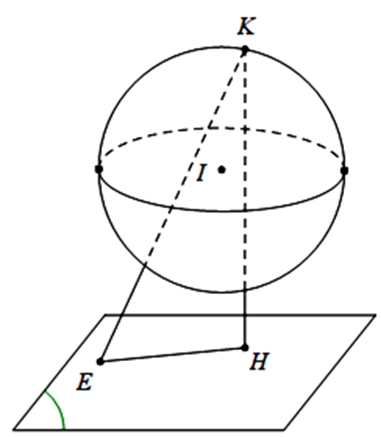
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {4;5;7} \right)\), bán kính \(R = \sqrt 2 \).
Giả sử trong mặt phẳng \(\left( {IAB} \right)\) tiếp tuyến tại A và B của \(\left( S \right)\) cắt nhau tại C thì IACB là hình vuông cạnh \(IA = R = \sqrt 2 \Rightarrow AB = IA\sqrt 2 = 2\), gọi K là trung điểm của AB thì \(IK = \frac{{AB}}{2} = 1\).
Điểm K thuộc mặt cầu \(\left( {S'} \right)\) tâm \(I\left( {4;5;7} \right)\), bán kính \(R' = 1\).
Gọi E là trung điểm của AB, vì ABNM là hình thang nên KE là đường trung bình của hình thang ABNM do đó \(AM + BN = 2KE\) trong \(K \in \left( {S'} \right)\) và
\(\overrightarrow {{u_{KE}}} = \overrightarrow {{u_d}} = \left( {2;1;1} \right) \Rightarrow KE\) luôn tạo với \(\left( {Oxy} \right):z = 0\) một góc \(\varphi \) không đổi và \(\sin \varphi = \frac{1}{{\sqrt 6 }}\).
Lại có: \[KE\sin \varphi = d\left( {K,(P)} \right) \Rightarrow KE = \sqrt 6 d\left( {K,(P)} \right) \le \sqrt 6 \left[ {d\left( {I;(Oxy)} \right) + R'} \right] = \sqrt 6 \left( {7 + 1} \right) = 8\sqrt 6 \]
Suy ra \(AM + BN = 2KE \le 16\sqrt 6 \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
