Có bao nhiêu giá trị nguyên của tham số m (với |m|<10 ) để phương trình

Đáp án C

Ta có: \({2^{x - 1}} = {\log _4}\left( {x + 2m} \right) + m \Leftrightarrow \frac{1}{2}{2^x} = {\log _{{2^2}}}\left( {x + 2m} \right) + m \Leftrightarrow {2^x} = {\log _2}\left( {x + 2m} \right) + 2m\)

Đặt \(y = {\log _2}\left( {x + 2m} \right)\) suy ra \({2^y} = x + 2m\)

Ta có hệ phương trình \(\left\{ \begin{array}{l}{2^x} = y + 2m\\{2^y} = x + 2m\end{array} \right. \Rightarrow {2^x} + x + 2m = {2^y} + y + 2m\) (cộng chéo) \( \Leftrightarrow {2^x} + x = {2^y} + y\) (*)

Xét hàm số \(f\left( t \right) = {2^t} + t{\rm{ }}\left( {t \in \mathbb{R}} \right)\) ta có: \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0{\rm{ }}\left( {\forall t \in \mathbb{R}} \right)\) suy ra hàm số \(f\left( t \right)\) đồng biến trên \(\mathbb{R}\).

Suy ra (*) \( \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y \Rightarrow {2^x} - x = 2m\)

Xét hàm số \(g\left( x \right) = {2^x} - x\) với \(x \in \mathbb{R}\) ta có: \(g'\left( x \right) = {2^x}\ln 2 - 1 = 0 \Leftrightarrow {2^x} = \frac{1}{{\ln 2}} \Leftrightarrow x = {\log _2}\frac{1}{{\ln 2}}\).

Ta có bảng biến thiên:

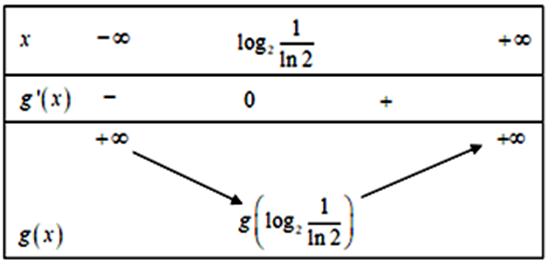
Phương trình đã cho có nghiệm khi và chỉ khi \(m \ge g\left( {{{\log }_2}\frac{1}{{\ln 2}}} \right) \approx 0,91\).

Kết hợp \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\\left| m \right| < 10\end{array} \right. \Rightarrow m = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\).