Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như sau
Câu hỏi :
Cho hàm số \[y = f\left( x \right)\]. Hàm số \[y = f'\left( x \right)\] có bảng biến thiên như sau:
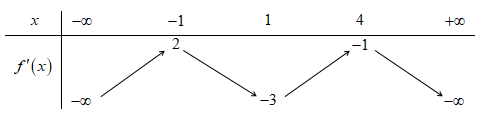
Bất phương trình \[f\left( {x + 2} \right) < x{e^x} + m\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi
Cho hàm số \[y = f\left( x \right)\]. Hàm số \[y = f'\left( x \right)\] có bảng biến thiên như sau:

Bất phương trình \[f\left( {x + 2} \right) < x{e^x} + m\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi
A. \[m > f\left( 1 \right) + \frac{1}{e}.\]
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Xét hàm số: \[g\left( x \right) = f\left( {x + 2} \right) - x{e^x},x \in \left( { - 1;1} \right) \Rightarrow g'\left( x \right) = f'\left( {x + 2} \right) - \left( {x + 1} \right){e^x}\].
Với mọi \[x \in \left( { - 1;1} \right)\] thì \[x + 2 \in \left( {1;3} \right) \Rightarrow f'\left( {x + 2} \right) < - 1 \Rightarrow f'\left( {x + 2} \right) < 0\].
Với mọi \[x \in \left( { - 1;1} \right)\] thì \[ - \left( {x + 1} \right){e^x} < 0 \Rightarrow g'\left( x \right) < 0,\forall x \in \left( { - 1;1} \right)\].
\[ \Rightarrow g\left( x \right)\] nghịch biến trên \[\left( { - 1;1} \right)\].
Khi đó \[m > g\left( x \right),\forall x \in \left( { - 1;1} \right) \Leftrightarrow m \ge g\left( { - 1} \right) \Leftrightarrow m \ge f\left( 1 \right) + \frac{1}{e}\].
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
