Từ một tấm tôn dạng hình tam giác vuông với hai cạnh góc vuông bằng

Đáp án A

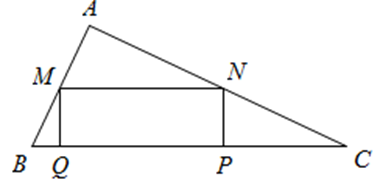
Khối trụ thu được có thể tích là \[V = \pi {R^2}h\].

\[\begin{array}{l}\Delta BQM\~\Delta BAC \Rightarrow \frac{{QM}}{{AC}} = \frac{{BQ}}{{BA}} \Rightarrow \frac{h}{4} = \frac{{BQ}}{3} \Rightarrow BQ = \frac{{3h}}{4}.\\\Delta CPN\~\Delta CAB \Rightarrow \frac{{PN}}{{AB}} = \frac{{CP}}{{CA}} \Rightarrow \frac{h}{4} = \frac{{CP}}{3} \Rightarrow CP = \frac{{4h}}{3}.\end{array}\]

Do đó \[PQ = BC - BQ - CP = 5 - \frac{{3h}}{4} - \frac{{4h}}{3} = 5 - \frac{{25h}}{{12}} = \frac{{60 - 25h}}{{12}}\].

Mà \[2R\pi = PQ \Rightarrow R = \frac{{60 - 25h}}{{24\pi }} \Rightarrow V = \pi {\left( {\frac{{60 - 25h}}{{24\pi }}} \right)^2}h = \frac{{h{{\left( {25h - 60} \right)}^2}}}{{{{24}^2}\pi }} = f\left( h \right)\].

\[f'\left( h \right) = \frac{{{{\left( {25h - 60} \right)}^2} + h.2\left( {25h - 60} \right).25}}{{{{24}^2}\pi }} = 0 \Rightarrow h = \frac{4}{5} \Rightarrow V \le f\left( {\frac{4}{5}} \right) \approx 0,71\;{m^3}.\]