Cho phương trình (căn x + căn (x+1))(m*căn x+1/(căn (x+1))

Đáp án D

Điều kiện \[x > 1\]. Phương trình \[ \Leftrightarrow m\sqrt x + \frac{1}{{\sqrt {x - 1} }} + 16\sqrt[4]{{{x^2} - x}} = \sqrt x - \sqrt {x - 1} \]

\[\begin{array}{l} \Leftrightarrow m + \frac{1}{{\sqrt x .\sqrt {x - 1} }} + 16.\frac{{\sqrt[4]{{{x^2} - x}}}}{{\sqrt x }} = 1 - \frac{{\sqrt {x - 1} }}{{\sqrt x }}\\ \Leftrightarrow m = - 16.\sqrt[4]{{\frac{{{x^2} - x}}{{{x^2}}}}} - \frac{{x - 1}}{{\sqrt {x\left( {x - 1} \right)} }} - \frac{1}{{\sqrt {x\left( {x - 1} \right)} }} + 1 \Leftrightarrow m = - 16.\sqrt[4]{{\frac{{x - 1}}{x}}} - \sqrt {\frac{x}{{x - 1}}} + 1.\end{array}\]

Đặt \[t = \sqrt[4]{{\frac{{x - 1}}{x}}} \in \left( {0;1} \right)\], ta có \[m = - 16t - \frac{1}{{{t^2}}} + 1\].

Xét hàm số \[f\left( t \right) = - 16t - \frac{1}{{{t^2} + 1}}\], với \[t \in \left( {0;1} \right)\] ta có \[f'\left( t \right) = - 16 + \frac{2}{{{t^3}}} = 0 \Rightarrow t = \frac{1}{2}\].

Xét bảng sau:

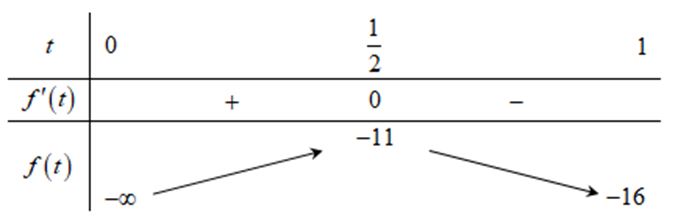
Từ đó ta được \[ - 16 < m < - 11\]. Mà \[m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 15; - 14; - 13; - 12} \right\}\].