Trong không gian Oxyz, cho mặt cầu (S): (x-1)^2+(y-1)^2+z^2=4

Đáp án A

Mặt cầu \[\left( S \right)\] có tâm \[I\left( {1;1;0} \right)\] và bán kính \[R = 2\].

Ta có \[\overrightarrow {IM} = \left( {1;2;1} \right) \Rightarrow IM = \sqrt 6 \]

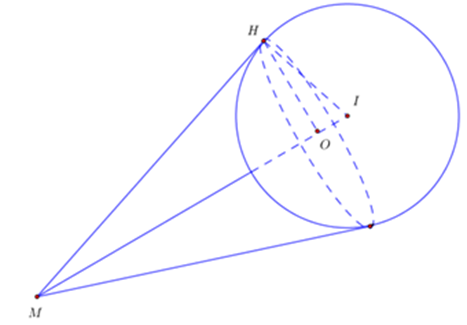
Gọi H là một tiếp điểm tùy ý khi kẻ tiếp tuyến từ M đến mặt cầu.

Kẻ  \[HO \bot IM\;\left( {O \in IM} \right)\], ta có \[IO.IM = H{I^2} \Rightarrow IO.\sqrt 6 = 4 \Rightarrow IO = \frac{{2\sqrt 6 }}{4}\].

Mà I, M cố định \[ \Rightarrow \] O cố định.

Ta có \[MH = \sqrt {I{M^2} - {R^2}} = \sqrt 2 \Rightarrow \frac{1}{{H{O^2}}} = \frac{1}{{M{H^2}}} + \frac{1}{{M{I^2}}} = \frac{1}{2} + \frac{1}{4} \Rightarrow OH = \frac{2}{{\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\].

Vậy \[\left( C \right)\] là đường tròn tâm O có bán kính \[r = OH = \frac{{2\sqrt 3 }}{3}\].