Cho Parabol P: y=x^2 và hai điểm A, B thuộc (P) sao cho AB=2

Đáp án C

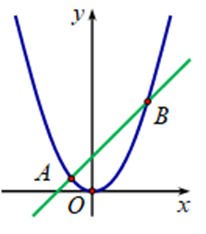
Xét \[A\left( {a;{a^2}} \right),B\left( {b;{b^2}} \right)\] với \[a < b\].

Ta có \[\overrightarrow {AB} = \left( {b - a;{b^2} - {a^2}} \right) \Rightarrow \overrightarrow {{n_{AB}}} = \left( {a + b; - 1} \right)\].

\[\begin{array}{l} \Rightarrow AB:\left( {a + b} \right)\left( {x - a} \right) - \left( {y - {a^2}} \right) = 0\\ \Rightarrow AB:y = \left( {a + b} \right)x - ab.\end{array}\]

Lại có \[AB = 2 \Leftrightarrow {\left( {b - a} \right)^2} + {\left( {{b^2} - {a^2}} \right)^2} = 4\].

Phương trình hoành độ giao điểm \[{x^2} = \left( {a + b} \right)x - ab \Leftrightarrow x\left( {x - a} \right) - b\left( {x - a} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\x = b\end{array} \right.\].

Diện tích hình phẳng giới hạn bởi \[\left( P \right):y = {x^2}\] và đường thẳng AB là

\[\begin{array}{l}S = \int\limits_a^b {\left| {\left( {x - a} \right)\left( {x - b} \right)} \right|dx} = - \int\limits_a^b {\left( {x - a} \right)\left( {x - b} \right)dx} = \int\limits_a^b {\left[ {\left( {a + b} \right)x - ab - {x^2}} \right]dx} \\ = \left[ {\left( {a + b} \right).\frac{{{x^2}}}{2} - abx - \frac{{{x^3}}}{3}} \right]\left| \begin{array}{l}^b\\_a\end{array} \right. = \frac{1}{2}\left( {a + b} \right)\left( {{b^2} - {a^2}} \right) - ab\left( {b - a} \right) - \frac{1}{3}\left( {{b^3} - {a^3}} \right)\\ = \left( {b - a} \right)\left[ {\frac{1}{2}{{\left( {a + b} \right)}^2} - ab - \frac{1}{3}\left( {{a^2} + ab + {b^2}} \right)} \right] = \left( {b - a} \right).\frac{{3{{\left( {a + b} \right)}^2} - 6ab - 2\left( {{a^2} + ab + {b^2}} \right)}}{6}\\ = \frac{1}{6}\left( {b - a} \right)\left( {{a^2} + {b^2} - 2ab} \right) = \frac{1}{6}{\left( {b - a} \right)^3}.\end{array}\]

Từ \[{\left( {b - a} \right)^2} + {\left( {{b^2} - {a^2}} \right)^2} = 4 \Rightarrow {\left( {b - a} \right)^2}\left( {1 + {{\left( {b + a} \right)}^2}} \right) = 4 \Rightarrow {\left( {b - a} \right)^2} = \frac{4}{{1 + {{\left( {b + a} \right)}^2}}} \le 4\]

\[ \Rightarrow b - a \le 2 \Rightarrow S = \frac{{{{\left( {b - a} \right)}^3}}}{6} \le \frac{{{2^3}}}{6} = \frac{4}{3}\].

Dấu “=” xảy ra \[ \Leftrightarrow \left\{ \begin{array}{l}a + b = 0\\b - a = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\a = - 1\end{array} \right. \Rightarrow A\left( { - 1;1} \right),B\left( {1;1} \right)\].