Trong không gian Oxyz, cho hai điểm B(2;-1;-3)
Câu hỏi :
Trong không gian Oxyz, cho hai điểm \[B\left( {2;{\mkern 1mu} - 1;{\mkern 1mu} - 3} \right)\], \[C\left( { - 6;{\mkern 1mu} - 1;{\mkern 1mu} {\mkern 1mu} 3} \right)\]. Trong các tam giác ABC thỏa mãn các đường trung tuyến kẻ từ B và C vuông góc với nhau, điểm \[A\left( {a;b;0} \right)\], (\[b > 0\]) sao cho giá trị của \[\cos A\] nhỏ nhất. Tính \[a + b.\]
* Đáp án
C
* Hướng dẫn giải
Đáp án C
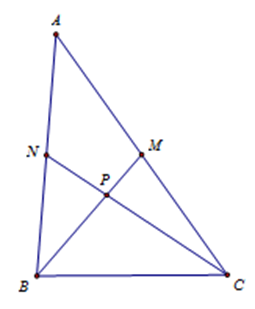
Gọi M, N lần lượt là trung điểm của các cạnh AC, AB.
Gọi \[P = BM \cap CN\], ta có \[BM \bot CN\] nên \[B{C^2} = B{P^2} + C{P^2}\].
Theo công thức tính đường trung tuyến, ta có:
\[\begin{array}{l}B{P^2} = {\left( {\frac{2}{3}BM} \right)^2} = \frac{4}{9}.\frac{{2\left( {B{A^2} + B{C^2}} \right) - A{C^2}}}{4}\\C{P^2} = {\left( {\frac{2}{3}CN} \right)^2} = \frac{4}{9}.\frac{{2\left( {C{A^2} + C{B^2}} \right) - A{B^2}}}{4}\\ \Rightarrow B{C^2} = \frac{{A{B^2} + A{C^2} + 4B{C^2}}}{9} \Rightarrow A{B^2} + A{C^2} = 5B{C^2}.\end{array}\]
Ta có \[\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{5\left( {A{B^2} + A{C^2}} \right) - \left( {A{B^2} + A{C^2}} \right)}}{{10.AB.AC}} = \frac{2}{5}.\frac{{A{B^2} + A{C^2}}}{{AB.AC}} \ge \frac{2}{5}.\frac{{2AB.AC}}{{AB.AC}} = \frac{4}{5}\].
Dấu “=” xảy ra \[ \Leftrightarrow AB = AC\].
Ta có \[A\left( {a;b;0} \right),b > 0\] và \[B\left( {2; - 1; - 3} \right),C\left( { - 6; - 1;3} \right)\].
\[ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} = \left( {2 - a; - 1 - b; - 3} \right) \Rightarrow A{B^2} = {\left( {2 - a} \right)^2} + {\left( {b + 1} \right)^2} + 9\\\overrightarrow {AC} = \left( { - 6 - a; - 1 - b;3} \right) \Rightarrow A{C^2} = {\left( {a + 6} \right)^2} + {\left( {b + 1} \right)^2} + 9\end{array} \right.\].
Ép cho \[A{B^2} = A{C^2} \Rightarrow 4 - 4a = 36 + 12a \Leftrightarrow a = - 2\].
Ta có \[\overrightarrow {BC} = \left( { - 8;0;6} \right) \Rightarrow B{C^2} = 100\]. Khi đó từ \[A{B^2} + A{C^2} = 5B{C^2}\] và \[AB = AC\]
\[ \Rightarrow 2\left[ {{{\left( {2 - a} \right)}^2} + {{\left( {b + 1} \right)}^2} + 9} \right] = 5.100 \Rightarrow {4^2} + {\left( {b + 1} \right)^2} + 9 = 250\].
Kết hợp với \[b > 0\] ta được \[b = 14\] thỏa mãn \[ \Rightarrow a + b = 12\].
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
