Trang chủ Đề thi & kiểm tra Khác Hàm số bậc hai !! Tìm giá trị nhỏ nhất của biểu thức P =

Tìm giá trị nhỏ nhất của biểu thức P =

Khác -

Giải toán 5 Ôn tập và bổ sung về giải toán tiếp theo !!

Giải VBT Toán 5 Bài 71: Luyện tập !!

Trắc nghiệm Tiếng Anh 9 Unit 9 Vocabulary and Grammar có đáp án !!

Khoa học 4 Bài 12: Phòng một số bệnh do thiếu chất dinh dưỡng !!

Khoa học 4 Bài 18 - 19: Ôn tập: Con người và sức khỏe !!

Trắc nghiệm Tiếng Anh 7 mới Unit 6 Writing có đáp án !!

VBT Tự nhiên và Xã hội 3 Bài 46: Khả năng kì diệu của lá cây !!

Bộ câu hỏi Nhanh như chớp !!

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 1 (Có đáp án)

Trắc nghiệm môn luật đất đai - Đề số 1 (Có đáp án)

Trắc nghiệm môn luật đất đai - Đề số 2 (Có đáp án)

Trắc nghiệm ngữ pháp Tiếng Anh tìm lỗi sai - Đề số 1 (Có đáp án)

Trắc nghiệm môn luật đất đai - Đề số 3 (Có đáp án)

Trắc nghiệm môn luật đất đai - Đề số 4 (Có đáp án)

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 2

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 3

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 4

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 5

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 6

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 7

Trắc nghiệm lý thuyết bằng lái xe máy A1 - Đề số 8

Đề thi nghề tin học THPT mã số 1

Đề thi nghề tin học THPT mã số 2

Câu hỏi trắc nghiệm Giáo dục quốc phòng an ninh phần 1

Đề thi nghề tin học THPT mã số 3

Câu hỏi :

Tìm giá trị nhỏ nhất của biểu thức $P = 3 (\frac{a^{2}}{b^{2}} + \frac{b^{2}}{a^{2}}) - 8 (\frac{a}{b} + \frac{b}{a})$

A. $- \frac{34}{3}$

B.4

C.22

D.−10

* Đáp án

* Hướng dẫn giải

Ta có :

{(\frac{a}{b} + \frac{b}{a})}^{2} = \frac{a^{2}}{b^{2}} + 2 \frac{a}{b} . \frac{b}{a} + \frac{b^{2}}{a^{2}} = \frac{a^{2}}{b^{2}} + \frac{b^{2}}{a^{2}} + 2 \Rightarrow \frac{a^{2}}{b^{2}} + \frac{b^{2}}{a^{2}} = {(\frac{a}{b} + \frac{b}{a})}^{2} - 2

Biến đổi biểu thức P về dạng

P = 3 {(\frac{a}{b} + \frac{b}{a})}^{2} - 6 - 8 (\frac{a}{b} + \frac{b}{a}) = 3 {(\frac{a}{b} + \frac{b}{a})}^{2} - 8 (\frac{a}{b} + \frac{b}{a}) - 6

Đặt

t = \frac{a}{b} + \frac{b}{a} \Rightarrow t^{2} = {(\frac{a}{b} + \frac{b}{a})}^{2}

Áp dụng bất đẳng thức

{(x + y)}^{2} \geq 4 x y \forall x, y

với hai số

\frac{a}{b}

và

\frac{b}{a}

ta có:

t^{2} = {(\frac{a}{b} + \frac{b}{a})}^{2} \geq 4 \frac{a}{b} . \frac{b}{a} = 4 \Leftrightarrow | t | \geq 2 \Leftrightarrow [\begin{matrix} t \geq 2 \\ t \leq - 2 \end{matrix}

Biểu thức P trở thành

P = 3 t^{2} - 8 t - 6

Trục đối xứng

x = - \frac{b}{2 a} = \frac{4}{3}

và hệ số

a = 3 > 0.

Suy ra hàm số

f (t) = 3 t^{2} - 8 t - 6

nghịch biến trên khoảng

(- \infty; \frac{4}{3})

và đồng biến trên khoảng

(\frac{4}{3}; + \infty)

BBT :

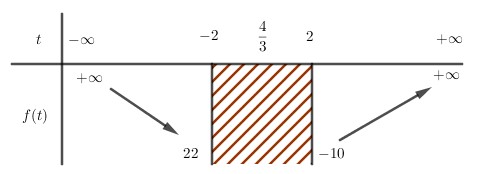
Tìm giá trị nhỏ nhất của biểu thức P = (ảnh 1)

Từ đây suy ra hàm số f(t) đạt giá trị nhỏ nhất tại t = 2
Ta có f(2 )= −10.
Vậy minP = minf(t) = −10.
Đáp án cần chọn là: D

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Hàm số bậc hai !!

Số câu hỏi: 54