Cho hình chóp S.ABC có các cạnh SA = SB = SC = 2a và đáy ABC là tam giác

Đáp án D

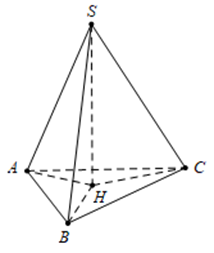
Kẻ \(SH \bot \left( {ABC} \right) \Rightarrow HA = HB = HC = \frac{{AB}}{{\sqrt 3 }} = a.\)

Ta có \(\widehat {\left( {SB;\left( {ABC} \right)} \right)} = \widehat {SBH}\)

\( \Rightarrow \cos \widehat {\left( {SB;\left( {ABC} \right)} \right)} = \cos \widehat {SBH} = \frac{{BH}}{{SB}} = \frac{a}{{2a}} = \frac{1}{2}\)

\( \Rightarrow \widehat {\left( {SB;\left( {ABC} \right)} \right)} = {60^0}.\)