Trong không gian, cho hình thang cân ABCD có đáy nhỏ AB = 1

Đáp án A

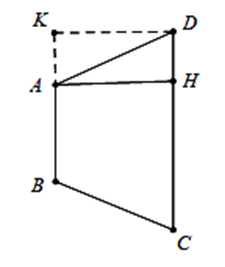
Ta có \(V = {V_{tru}} - 2{V_{non}} = \pi {r^2}h - 2.\frac{1}{3}\pi {R^2}h' = \pi .K{D^2}.CD - \frac{2}{3}\pi K{D^2}.AK.\)

Cạnh \(AK = DH = \frac{{CD - AB}}{2} = 1\)

\( \Rightarrow K{D^2} = A{D^2} - A{K^2} = 1 \Rightarrow V = \frac{7}{3}\pi .\)