Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Cho hình lăng trụ tam giác đều ABC.A'B'C' Góc giữa...
Cho hình lăng trụ tam giác đều ABC.A'B'C' Góc giữa hai mặt phẳng
Câu hỏi :
Cho hình lăng trụ tam giác đều \[ABC.A'B'C'.\] Góc giữa hai mặt phẳng \[\left( {A'BC} \right)\] và \[\left( {ABC} \right)\]bằng \[30^\circ .\] Tam giác \[A'BC\] có diện tích bằng 8. Tính thể tích khối lăng trụ \[ABC.A'B'C'.\]
A. \[8\sqrt 3 .\]
B. \[8\sqrt 2 .\]
C. 8.
D. 6.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
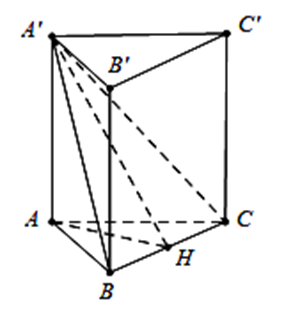
Kẻ \(AH \bot BC \Rightarrow \widehat {\left( {(A'BC);(ABC)} \right)} = \widehat {A'HA} = 30^\circ \)
\( \Rightarrow \cos 30^\circ = \frac{{AH}}{{A'H}} = \frac{{\sqrt 3 }}{2} \Rightarrow A'H = \frac{2}{{\sqrt 3 }}AH = \frac{2}{{\sqrt 3 }}.\frac{{AB\sqrt 3 }}{2} = AB\).
\({S_{A'BC}} = \frac{1}{2}BC.A'H = \frac{1}{2}AB.AB = 8 \Rightarrow AB = 4\).
\(\tan 30^\circ = \frac{{A'A}}{{AH}} = \frac{{A'A}}{{\frac{{AB\sqrt 3 }}{2}}} \Rightarrow A'A = 2\)
\( \Rightarrow V = A'A.{S_{ABC}} = A'A.\frac{{A{B^2}\sqrt 3 }}{4} = 8\sqrt 3 \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Số câu hỏi: 1086
Copyright © 2021 HOCTAP247
