Cho hình nón (N) có đường sinh bằng a, góc ở đỉnh bằng 90 độ

Đáp án A

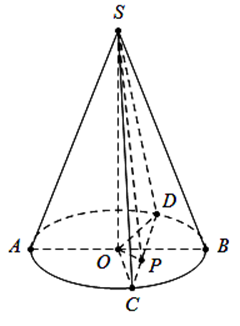
\(\Delta SAB\) vuông cân tại \(S \Rightarrow SO = OA = OB = \frac{a}{{\sqrt 2 }}\).

Thiết diện qua đỉnh của \(\left( N \right)\) là \(\Delta SC{\rm{D}}\) như hình vẽ.

Kẻ \(OP \bot C{\rm{D}} \Rightarrow \widehat {\left( {(SC{\rm{D}});(OC{\rm{D}})} \right)} = \widehat {SPO} = 60^\circ \).

\(\sin 60^\circ = \frac{{SO}}{{SP}} = \frac{{\sqrt 3 }}{2} \Rightarrow SP = \frac{2}{{\sqrt 3 }}.SO = \frac{2}{{\sqrt 3 }}.\frac{a}{{\sqrt 2 }} = a\sqrt {\frac{2}{3}} \).

\(\tan 60^\circ = \frac{{SO}}{{OP}} \Rightarrow OP = \frac{{SO}}{{\sqrt 3 }} = \frac{a}{{\sqrt 6 }}\)

\( \Rightarrow P{\rm{D}} = \sqrt {O{{\rm{D}}^2} - O{P^2}} = \sqrt {{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2} - {{\left( {\frac{a}{{\sqrt 6 }}} \right)}^2}} = \frac{a}{{\sqrt 3 }}\)

\( \Rightarrow C{\rm{D}} = 2P{\rm{D}} = \frac{{2{\rm{a}}}}{{\sqrt 3 }} \Rightarrow {S_{SC{\rm{D}}}} = \frac{1}{2}SP.C{\rm{D}} = \frac{{{a^2}\sqrt 2 }}{3}\).