Cho a,b là các số thực dương thỏa mãn b>1

Đáp án C

Ta có \(P = \frac{1}{{{{\log }_a}\frac{a}{b}}} + 4{\log _b}\frac{a}{b} = \frac{1}{{1 - {{\log }_a}b}} + 4\left( {{{\log }_b}a - 1} \right) = \frac{1}{{1 - {{\log }_a}b}} + \frac{4}{{{{\log }_a}b}} - 4.\)

Đặt \(t = {\log _a}b \Rightarrow P = \frac{1}{{1 - t}} + \frac{4}{t} - 4.\)

Từ \(a > \sqrt a \Rightarrow a > 1 \Rightarrow t = {\log _a}b < {\log _a}a \Rightarrow t < 1.\)

Từ \(b \ge \sqrt a \Rightarrow t = {\log _a}b \ge {\log _a}\sqrt a = \frac{1}{2} \Rightarrow \frac{1}{2} \le t < 1.\)

Xét hàm số \(f\left( t \right) = \frac{1}{{1 - t}} + \frac{4}{t} - 4\), với \(t \in \left[ {\frac{1}{2};1} \right)\) có \(\left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{f'\left( t \right) = \frac{1}{{{{\left( {1 - t} \right)}^2}}} - \frac{4}{{{t^2}}} = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{t = 2\left( {1 - t} \right)}\end{array}} \right. \Leftrightarrow t = \frac{2}{3}.\)

Xét bảng sau:

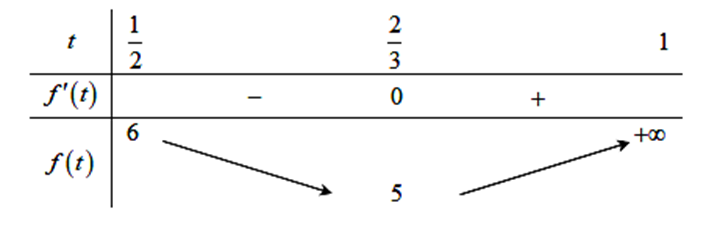
Từ đó \(\mathop {\min }\limits_{\left[ {\frac{1}{2};1} \right)} f\left( t \right) = 5\).