Cho hình phẳng (H) giới hạn bởi các đường y= căn bậc 2 của x

Đáp án C

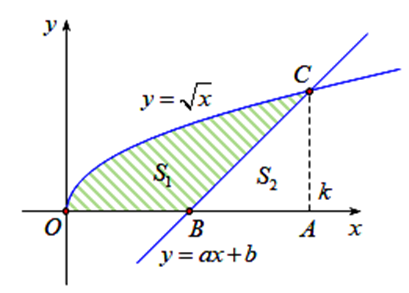
Ta có: \({S_1} + {S_2} = \int\limits_0^k {\sqrt x dx} = \int\limits_0^{\sqrt k } {td\left( {{t^2}} \right)} = \int\limits_0^{\sqrt k } {t.2tdt} = \frac{{2k\sqrt k }}{3}.\)

\({S_2} = \frac{1}{2}AC.AB = \frac{1}{2}\sqrt k .\frac{k}{2} = \frac{1}{4}k\sqrt k \)

\( \Rightarrow {S_1} = \frac{2}{3}k\sqrt k - \frac{1}{4}k\sqrt k = \frac{5}{{12}}k\sqrt k \)

\( \Rightarrow 3{S_1} + {S_2} = \frac{3}{2}k\sqrt k = 12 \Rightarrow k = 4.\)

Đường thẳng \(y = ax + b\) qua

\(B\left( {2;0} \right),C\left( {4;2} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2a + b = 0}\\{4a + b = 2}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 2}\end{array}} \right..\)