Cho ba số phức z1,z2,z3 thỏa mãn |z1|=|z2|=|z3|=1

Đáp án D

Gọi M, N, P lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2},{z_3}\).

Suy ra M, N, P thuộc đường tròn \(\left( {O;1} \right)\).

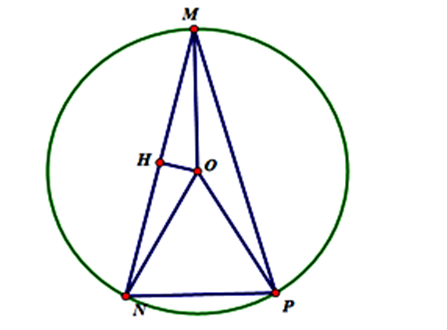
Ta có \(MN = \left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\).

Kẻ \(OH \bot MN \Rightarrow MH = \frac{{MN}}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4} \Rightarrow \cos \widehat {OMN} = \frac{{MN}}{{OM}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)

\( \Rightarrow \widehat {OMN} = {15^0} \Rightarrow \widehat {MON} = {150^0}\)

Ta có \(\left| {{z_3} - {z_1}} \right| = \left| {{z_1}} \right|.\left| {{z_3} - {z_1}} \right| = \left| {{z_3}{z_1} - z_1^2} \right| = \left| {{z_3}{z_1} - {z_3}{z_2}} \right| = \left| {{z_3}} \right|.\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\)

\( \Rightarrow MP = \left| {{z_3} - {z_1}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2} \Rightarrow MN = MP = \frac{{\sqrt 6 + \sqrt 2 }}{2}.\)

Tương tự như trên \( \Rightarrow \widehat {MOP} = {150^0} \Rightarrow \widehat {NOP} = {360^0} - \left( {{{150}^0} + {{150}^0}} \right) = {60^0}\)

\( \Rightarrow \Delta NOP\) đều \( \Rightarrow NP = 1\)

\( \Rightarrow \left| {{z_2} - {z_3}} \right| = NP = 1 \Rightarrow \left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right| = 1 - \frac{{\sqrt 6 + \sqrt 2 }}{2} = \frac{{2 - \sqrt 6 - \sqrt 2 }}{2}.\)