Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Cho hình nón có đỉnh S và đáy là đường...
Cho hình nón có đỉnh S và đáy là đường tròn (O;R)
Câu hỏi :
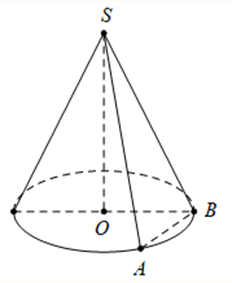
Cho hình nón có đỉnh S và đáy là đường tròn \[\left( {O;R} \right)\]. Trên đường tròn \[\left( {O;R} \right)\] lấy hai điểm \[A,{\rm{ }}B\] sao cho tam giác \[OAB\] vuông. Biết diện tích tam giác SAB bằng \[{R^2}\sqrt 2 .\] Tính thể tích V của khối nón đã cho.
A. \[V = \frac{{\pi {R^3}\sqrt {14} }}{2}\]
B. \[V = \frac{{\pi {R^3}\sqrt {14} }}{3}\]
C. \[V = \frac{{\pi {R^3}\sqrt {14} }}{6}\]
D. \[V = \frac{{\pi {R^3}\sqrt {14} }}{{12}}\]
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Ta có \[OA = OB \Rightarrow OA \bot OB \Rightarrow AB = R\sqrt 2 \].
\[{S_{SAB}} = \frac{1}{2}AB\sqrt {S{A^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = {R^2}\sqrt 2 \].
\[\begin{array}{l} \Rightarrow \frac{1}{2}.R\sqrt 2 = \sqrt {S{A^2} - {{\left( {\frac{{R\sqrt 2 }}{2}} \right)}^2}} = {R^2}\sqrt 2 \\ \Rightarrow S{A^2} - \frac{{{R^2}}}{2} = \left( {2{R^2}} \right) \Rightarrow SA = \frac{{3R}}{{\sqrt 2 }}\\ \Rightarrow h = SO = \sqrt {S{A^2} - {R^2}} = R\sqrt {\frac{7}{2}} \Rightarrow V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\sqrt {\frac{7}{2}} \pi {R^3}.\end{array}\]
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Số câu hỏi: 1086
Copyright © 2021 HOCTAP247
